Correlation Studies

The “personality” of correlations may be of particular interest to asset allocation strategists because research demonstrates that a more active approach to how we view and use the correlation statistic can materially impact results. Indeed, investments are often assesed using correlation of monthly returns between two asset classes; however, daily or other time-frames can be used. Some analysts have shown that the correlations between various asset classes have drifted over time, whereas some investment practitioners say that a long- term perspective is warranted.

Correlation Studies: some examples

In order to study the stability and cyclical nature of the correlation measure, it is important to underline that the minimum and maximum correlation measures for the same data set can vary tremendously:

• Small-cap stocks and the S&P 500 are usually relatively high correlated at 0.82.
• Historically, large-cap and small-cap stocks have had a relatively high correlation. The correlation over the past ten years varies from a minimum of 84.5% at 241 days, to a maximum of 97.3% at 177 days.
• Historically, bonds and stocks have had a positive relationship, with correlations on the order of 0.40. However, over the past ten years, stocks have struggled during various financial crises, while interest rates have declined (and bonds have risen) during the same period. As a result, stocks and bonds have had a negative correlation over the past ten years.
• Correlations amongst global stocks have risen over the years, along with increased globalization. In this case, the correlations are relatively stable as a function of the number of days.
• The relationship between stocks and commodities can be described by relatively low correlations – that are fairly variable and volatile (as a function of the number of days). Again, we see a large variation in correlation computations.

In general, MPT practitioners consider the correlation of monthly returns (about 20 trading days) as more conservative (i.e., has lower correlations) than longer-term and average calculations. However, a slightly longer-term perspective such as 60 trading-days captures more meaningful relationships amongst asset classes. When considering the long-term perspective (i.e., rolling five-year correlations of quarterly performance between several sets of assets), correlations amongst asset classes are not very related and shows different reactions during market cycles and market events (have a personality of their own ). However, it is important to note that:

• correlations can be a moving target because they may drift and even converge towards 1.00 like in the case of global stocks because the world’s economy has become increasingly global (Chin 2010).
• Distress in the financial markets typically drives correlations higher during times of economic stress because of the rush towards liquidity.

Consider the case of the S&P500 and the VIX indexes. In general, when the S&P500 rises the VIX falls possibly because when the stock market advances investors are calm, do not trade much, and long-only traders ride the wave; instead when the stock market declines, trading volume increases and volatility increases as well.

Copulas

Consider a stock exchange with 77 firms. The table below represents the joint distribution of the variables “returns” and “prices”. For instance, there are 20 firms out of 77 that have positive returns of 2% AND price increase above the 180 days mean. The “Total” column represents the marginal distribution of prices, whereas the “Total” row represents the marginal distribution of returns. For instance, there are 31 firms out of 77 having a price increase above the 180 days mean; alternatively, there are 30 firms out of 77 showing positive returns of 2%. Finally, the column “Positive returns of 2%” represents the conditional distribution of prices given some specific returns; that is, given positive returns of 2%, 20 out of 30 firms have a price increase above the 180 days mean.

	Positive Return of 1%	Positive Return of 2%	Negative Return of 5%	Total
Price increase above the 20 days mean	3	5	3	11
Price Increase above the 180 days mean	10	20	1	31
Price Decrease below the 4 years mean	8	5	22	35
Total	21	30	26	77

Copulas allow to decompose a joint probability distribution into their marginals and also to specify a function (the copula) which couples marginals together and which permits to specify the correlation. Therefore, Copulas can be used to model situations of the joint distribution like:

• a specific correlation structure is given and we want to understand what happens to the marginal distributions.
• specific marginal distributions are given and we want to understand which correlation structure may result.
• given correlation structure and marginals, we want to select the copula best fitting the data

Specifically, a copula is a multivariate cumulative distribution function for which the marginal probability distribution of each variable is uniform. Sklar’s theorem states that any multivariate joint distribution can be written in terms of univariate marginal distribution functions and a copula which describes the dependence structure between the variables. Indeed, in various cases, functions exist that map from the uniform marginals to other marginal distributions.

Note that copulas mainly work when time series are stationary and continuous. Thus, a very important pre-processing step is to check for the auto-correlation, trend, and seasonality withing time series. Indeed, when time series are auto-correlated, copulas may generate a not existent dependence in the sets of variables and result in an incorrect dependence structure.

I consider again the S&P500 and VIX’s relation with the aim of introducing Copulas. First, a marginal distribution is fitted to each sample. Second, for each fitted marginal the inverse CDF function mapping to normal is plotted (a prerequisite for finding a suitable copula). Third, the joint distribution with normal marginals and -0.73 correlation is plotted. Fourth, the joint distribution with fitted marginals is plotted.

In the diagrams below, a selection of possible correlations of the joint distribution are represented in each of the six big graphs; instead, the smaller ones show how the correlation changes with different (mapped) marginals.

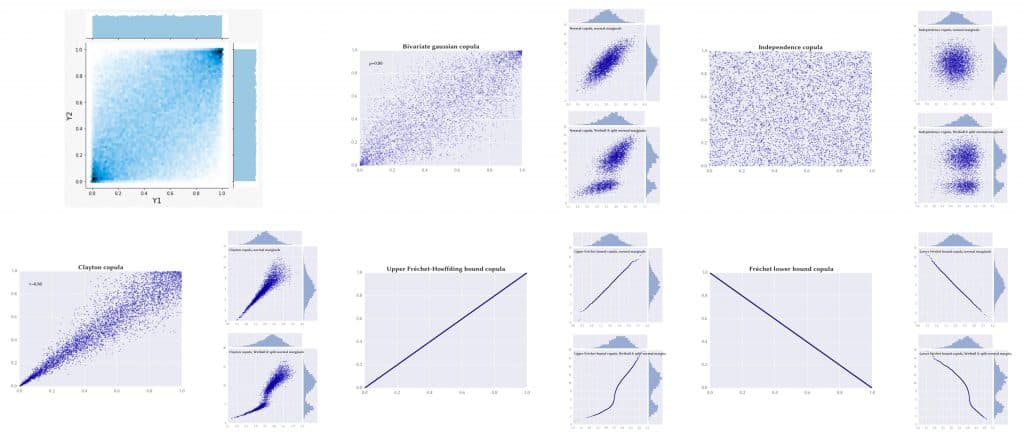
The Clayton copula allows for the occurrence of extreme downside events and is able to reduce the effects of extreme downside correlations compared to the Gaussian and Student-t copula.

References

Chin (2003). Correlations Have Personality, Too: An Analysis of Correlations between Assets

Marsden (2018). Copula and Multivariate Dependencies

Wiecky (2018). An intuitive, visual guide to Copulas